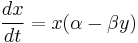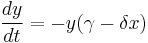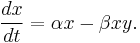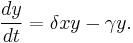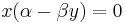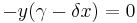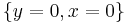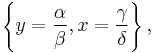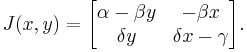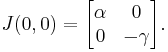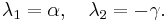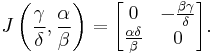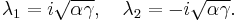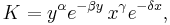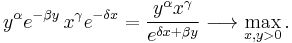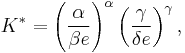Lotka–Volterra equation
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order, non-linear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey. They evolve in time according to the pair of equations:
where,
- y is the number of some predator (for example, foxes);
- x is the number of its prey (for example, rabbits);
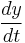 and
and 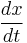 represent the growth of the two populations against time;
represent the growth of the two populations against time;- t represents the time; and
- α, β, γ and δ are parameters representing the interaction of the two species.
The Lotka–Volterra system of equations is an example of a Kolmogorov model,[1][2][3] which is a more general framework that can model the dynamics of ecological systems with predator-prey interactions, competition, disease, and mutualism.
Contents |
History
The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka “in the theory of autocatalytic chemical reactions” in 1910.[4][5] This was effectively the logistic equation,[6] which was originally derived by Pierre François Verhulst.[7] In 1920 Lotka extended, via Kolmogorov (see above), the model to "organic systems" using a plant species and a herbivorous animal species as an example [8] and in 1925 he utilised the equations to analyse predator-prey interactions in his book on biomathematics [9] arriving at the equations that we know today. Vito Volterra, who made a statistical analysis of fish catches in the Adriatic [5] independently investigated the equations in 1926.[10][11]
C.S. Holling extended this model yet again, in two 1959 papers, in which he proposed the idea of functional response.[12][13] Both the Lotka-Volterra model and Holling's extensions have been used to model the moose and wolf populations in Isle Royale National Park,[14] which with over 50 published papers is one of the best studied predator-prey relationships.
In economics
The Lotka–Volterra equations have a long history of use in economic theory; their initial application is commonly credited to Richard Goodwin in 1965[15] or 1967.[16][17] In economics, links are between many if not all industries; a proposed way to model the dynamics of various industries has been by introducing trophic functions between various sectors,[18] and ignoring smaller sectors by considering the interactions of only two industrial sectors.[19]
Physical meanings of the equations
The Lotka-Volterra model makes a number of assumptions about the environment and evolution of the predator and prey populations:
- The prey population finds ample food at all times.
- The food supply of the predator population depends entirely on the prey populations.
- The rate of change of population is proportional to its size.
- During the process, the environment does not change in favour of one species and the genetic adaptation is sufficiently slow.
As differential equations are used, the solution is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.[20]
Prey
When multiplied out, the prey equation becomes:
The prey are assumed to have an unlimited food supply, and to reproduce exponentially unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet; this is represented above by βxy. If either x or y is zero then there can be no predation.
With these two terms the equation above can be interpreted as: the change in the prey's numbers is given by its own growth minus the rate at which it is preyed upon.
Predators
The predator equation becomes:
In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). γy represents the loss rate of the predators due to either natural death or emigration; it leads to an exponential decay in the absence of prey.
Hence the equation expresses the change in the predator population as growth fueled by the food supply, minus natural death.
Solutions to the equations
The equations have periodic solutions which do not have a simple expression in terms of the usual trigonometric functions. However, a linearization of the equations yields a solution similar to simple harmonic motion[21] with the population of predators following that of prey by 90°.
An example problem
Suppose there are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 80 baboons and 40 cheetahs, one can plot the progression of the two species over time. The choice of time interval is arbitrary.
One can also plot a solution which corresponds to the oscillatory nature of the population of the two species. This solution is in a state of dynamic equilibrium. At any given time in this phase plane, the system is in a limit cycle and lies somewhere on the inside of these elliptical solutions. There is no particular requirement on the system to begin within a limit cycle and thus in a stable solution, however, it will always reach one eventually.
These graphs clearly illustrate a serious problem with this as a biological model: in each cycle, the baboon population is reduced to extremely low numbers yet recovers (while the cheetah population remains sizeable at the lowest baboon density). Given chance fluctuations, discrete numbers of individuals, and the family structure and lifecycle of baboons, the baboons actually go extinct and by consequence the cheetahs as well. This modelling problem has been called the "atto-fox problem",[22] an atto-fox being an imaginary 10−18 of a fox, in relation to rabies modelling in the UK.
Dynamics of the system
In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low the prey population will increase again. These dynamics continue in a cycle of growth and decline.
Population equilibrium
Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0.
When solved for x and y the above system of equations yields
and
Hence, there are two equilibria.
The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters, α, β, γ, and δ.
Stability of the fixed points
The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives, while the other fixed point requires a slightly more sophisticated method.
The Jacobian matrix of the predator-prey model is
First fixed point
When evaluated at the steady state of (0, 0) the Jacobian matrix J becomes
The eigenvalues of this matrix are
In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.
The stability of this fixed point is of importance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, we find that the extinction of both species is difficult in the model. (In fact, this can only occur if the prey are artificially completely eradicated, causing the predators to die of starvation. If the predators are eradicated, the prey population grows without bound in this simple model).
Second fixed point
Evaluating J at the second fixed point we get
The eigenvalues of this matrix are
As the eigenvalues are both purely imaginary, this fixed point is not hyperbolic, so no conclusions can be drawn from the linear analysis. However, the system admits a constant of motion
and the level curves, where K = const, are closed trajectories surrounding the fixed point. Consequently, the levels of the predator and prey populations cycle, and oscillate around this fixed point.
The largest value of the constant K can be obtained by solving the optimization problem
The maximal value of K is attained at the stationary point 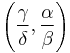 and it is given by
and it is given by
where e is Euler's Number.
See also
- Competitive Lotka–Volterra equations
- Generalized Lotka–Volterra equation
- Mutualism and the Lotka–Volterra equation
- Community matrix
- Population dynamics
- Population dynamics of fisheries
- Nicholson–Bailey model
Notes
- ^ Freedman, H.I., Deterministic Mathematical Models in Population Ecology, Marcel Dekker, (1980)
- ^ Brauer, F. and Castillo-Chavez, C., Mathematical Models in Population Biology and Epidemiology, Springer-Verlag, (2000)
- ^ Hoppensteadt, F., "Predator-prey model", Scholarpedia, 1(10), 1563, (2006)
- ^ Lotka, A.J., "Contribution to the Theory of Periodic Reaction", J. Phys. Chem., 14 (3), pp 271–274 (1910)
- ^ a b Goel, N.S. et al., “On the Volterra and Other Non-Linear Models of Interacting Populations”, Academic Press Inc., (1971)
- ^ Berryman, A.A., "The Origins and Evolution of Predator-Prey Theory", Ecology, 73(5), 1530-1535, (1992)
- ^ Verhulst, P.H., "Notice sur la loi que la population poursuit dans son accroissement". Corresp. mathématique et physique 10, 113–121, (1838)
- ^ Lotka, A.J., "Analytical Note on Certain Rhythmic Relations in Organic Systems”, Proc. Natl. Acad. Sci. U.S., 6, 410-415, (1920)
- ^ Lotka, A.J., Elements of Physical Biology, Williams and Wilkins, (1925)
- ^ Volterra, V., “Variazioni e fluttuazioni del numero d’individui in specie animali conviventi”, Mem. Acad. Lincei Roma, 2, 31-113, (1926)
- ^ Volterra, V., Variations and fluctuations of the number of individuals in animal species living together in Animal Ecology, Chapman, R.N. (ed), McGraw–Hill, (1931)
- ^ Holling, C.S., "The components of predation as revealed by a study of small mammal predation of the European Pine Sawfly", Can. Ent, 91, 293-320, (1959a)
- ^ Holling, C.S., “Some characteristics of simple types of predation and parasitism”, Can. Ent, 91, 385-398, (1959b)
- ^ Jost, C., Devulder, G., Vucetich, J.A., Peterson, R., and Arditi, R., "The wolves of Isle Royale display scale-invariant satiation and density dependent predation on moose", J. Anim. Ecol., 74(5), 809-816 (2005)
- ^ Gandolfo, G., "Giuseppe Palomba and the Lotka-Volterra equations", Rendiconti Lincei, 19(4), 347-257, (2008)
- ^ Goodwin, R.M. , "A Growth Cycle", Socialism, Capitalism and Economic Growth, Feinstein, C.H. (ed.), Cambridge University Press, (1967)
- ^ Desai, M. and Ormerod, P. "Richard Goodwin: A Short Appreciation", The Economic Journal, 108(450), 1431-1435 (1998)
- ^ Nasritdinov, G. and Dalimov, R.T., "Limit cycle, trophic function and the dynamics of intersectoral interaction", Current Research J. of Economic Theory, 2(2), 32-40, (2010)
- ^ Haken, H., Synergetics: introduction and advanced topics, Springer-Verlag, (2004)
- ^ Cooke, D. and Hiorns, R.W. et al., The Mathematical Theory of the Dynamics of Biological Populations II, Academic Press Inc., (1981)
- ^ Tong, H., Threshold Models in Non-linear Time Series Analysis, Springer–Verlag, (1983)
- ^ Mollison, D., "Dependence of epidemic and population velocities on basic parameters", Math. Biosci., 107, 255-287, (1991)
References
- E. R. Leigh (1968) The ecological role of Volterra's equations, in Some Mathematical Problems in Biology – a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
- Understanding Nonlinear Dynamics. Daniel Kaplan and Leon Glass.
- J.D. Murray. Mathematical Biology I: An Introduction. Springer-Verlag, 2003
External links
- Lotka–Volterra Predator-Prey Model by Elmer G. Wiens
- Lotka-Volterra Model
- NANIA Lotka-Volterra applet
- Lotka Algorithmic Simulation Similar program, in Javascript (requires an HTML5 browser).
- From the Wolfram Demonstrations Project — requires CDF player (free):